Contents
Ejercicio 1
Imprimir una tabla formateada (entero y real) del logaritmo natural de los numeros 10, 20, 40, 60 y 80. Sugerencia: usar el comando fprintf y vectores
format short x=[10 20 40 60 80]'; y=[x log(x)]; fprintf(' Numero\tln(Numero)\n'); fprintf('%5d \t %.4f\n',y');
Numero ln(Numero) 10 2.3026 20 2.9957 40 3.6889 60 4.0943 80 4.3820
Ejercicio 2
IMC Tenemos una función en otro fichero donde a la que llamaremos para este ejercicio. La recogemos a continuación:
% function [val msg] = imc(peso, est) % % val=peso/est^2; % if val<16 % msg='Infrapeso:Delgadez Severa'; % elseif val<17 % msg='Infrapeso:Delgadez Moderada'; % elseif val<18.5 % msg='Infrapeso:Delgadez Aceptable'; % elseif val<25 % msg='Peso Normal'; % elseif val<30 % msg='Sobrepeso'; % elseif val<35 % msg='Obeso: Tipo I'; % elseif val<40 % msg='Obeso: Tipo II'; % else % msg='Obeso: Tipo III'; % end % Hacemos un par de pruebas para poder mostrar su funcionamiento: [val,msg]=imc(80,1.60) [val,msg]=imc(90,1.5) [val,msg]=imc(70,1.8) [val,msg]=imc(70,1.93) [val,msg]=imc(40,1.60) [val,msg]=imc(40,1.50) % No se puede mostrar un programa que realice esto de forma reiterada hasta % que se permita finalización.
val =
31.2500
msg =
'Obeso: Tipo I'
val =
40
msg =
'Obeso: Tipo III'
val =
21.6049
msg =
'Peso Normal'
val =
18.7925
msg =
'Peso Normal'
val =
15.6250
msg =
'Infrapeso:Delgadez Severa'
val =
17.7778
msg =
'Infrapeso:Delgadez Aceptable'
Ejercicio 3
fprintf('10 base 2\t') cambia_base(10,2) fprintf('\n245 base 4\t') cambia_base(245,4) fprintf('\n60 base 7\t') cambia_base(60,7) fprintf('\n689 base 14\t') cambia_base(689,14) fprintf('\n')
10 base 2 1010 245 base 4 3311 60 base 7 114 689 base 14 373
Ejercicio 4
Método de Newton Introducimos la función y su derivada
f=inline('x.^3-sin(x)') df=inline('3*x^2-cos(x)') % Para realizar la tarea deseada se ha escrito una función recursiva que % calcula de manera autónoma el método de Newton. Se recoge a continuación. % function [ ans ] = newtonrec( f , df , x , tol) % %newtonrec Newton recursivo por JMAD % % Función que nos obtiene el valor de una raíz mediante el método de % % newton recogido de forma recursiva % % f es la función; df, su derivada; x, el valor inicial; y tol, el error % fx=f(x); % dfx=df(x); % if abs(fx)<tol % ans = x; % elseif ( abs(dfx)== 0 | fx==0 ) % ans= 'No tiene solución con ese valor inicial'; % else % x=x-fx/dfx; % ans= newtonrec(f,df,x,tol); % end % Introducimos cada valor inicial en la función recursiva xo=[-0.75,-0.5,0,.5,1.4]; x1=newtonrec(f,df,xo(1),10^-10); x2=newtonrec(f,df,xo(2),10^-10); x3=newtonrec(f,df,xo(3),10^-10); x4=newtonrec(f,df,xo(4),10^-10); x5=newtonrec(f,df,xo(5),10^-10); x=[x1,x2,x3,x4,x5]; fx=f(x); resultados=[xo' x' fx'] fprintf('Valor inicial\tValor final\tFunción en ese punto\n') for i=1:5 fprintf(' %.2f \t %.5f \t %2d \n',resultados(i,:)) end
f =
Inline function:
f(x) = x.^3-sin(x)
df =
Inline function:
df(x) = 3*x^2-cos(x)
resultados =
-0.7500 -0.9286 -0.0000
-0.5000 0.9286 0
0 0 0
0.5000 -0.9286 0
1.4000 0.9286 0.0000
Valor inicial Valor final Función en ese punto
-0.75 -0.92863 -1.265654e-14
-0.50 0.92863 0
0.00 0.00000 0
0.50 -0.92863 0
1.40 0.92863 2.875866e-11
Ejercicio 5
Refrigeración
A = [100 0 0 0 -1 1 0;0 200 0 0 0 -1 1;0 0 50 0 -1 0 0;0 0 0 100 0 -1 0;
0 300 0 0 0 0 -1;1 0 1 0 0 0 0;1 -1 0 -1 0 0 0]
b = [0 0 -50 -50 -50 25 0]'
% Introducidos los datos resolvemos el sistema
X = A \ b
A =
100 0 0 0 -1 1 0
0 200 0 0 0 -1 1
0 0 50 0 -1 0 0
0 0 0 100 0 -1 0
0 300 0 0 0 0 -1
1 0 1 0 0 0 0
1 -1 0 -1 0 0 0
b =
0
0
-50
-50
-50
25
0
X =
1.0e+03 *
0.0054
0.0009
0.0196
0.0045
1.0321
0.4964
0.3179
Ejercicio 6
Diferentes condiciones sobre la matriz del ejercicio anterior
A = [100 0 0 0 -1 1 0;0 200 0 0 0 -1 1;0 0 50 0 -1 0 0;0 0 0 100 0 -1 0;
0 300 0 0 0 0 -1;1 0 1 0 0 0 0;1 -1 0 -1 0 0 0];
% Número de condición
numcondicion = cond(A)
% Norma 1
n1 = norm(A,1)
% Norma 2
n2 = norm(A)
% Norma infinito
ninf=norm(A,Inf)
%Norma frobenius
nfrobenius=norm(A,'fro')
% Factorización LU
[L U] = lu(A)
% Volvemos a introducir b por si acaso
b = [0 0 -50 -50 -50 25 0]';
% Aplicamos
X = U^-1*L^-1*b
numcondicion =
2.6488e+04
n1 =
501
n2 =
360.5570
ninf =
301
nfrobenius =
390.5278
L =
1.0000 0 0 0 0 0 0
0 0.6667 0 0 0 1.0000 0
0 0 1.0000 0 0 0 0
0 0 0 1.0000 0 0 0
0 1.0000 0 0 0 0 0
0.0100 0 0.0200 0 1.0000 0 0
0.0100 -0.0033 0 -0.0100 0.3333 0.0167 1.0000
U =
100.0000 0 0 0 -1.0000 1.0000 0
0 300.0000 0 0 0 0 -1.0000
0 0 50.0000 0 -1.0000 0 0
0 0 0 100.0000 0 -1.0000 0
0 0 0 0 0.0300 -0.0100 0
0 0 0 0 0 -1.0000 1.6667
0 0 0 0 0 0 -0.0311
X =
1.0e+03 *
0.0054
0.0009
0.0196
0.0045
1.0321
0.4964
0.3179
Ejercicio 7
Autovalores y autovectores de la matriz
A = [0 1 -1;-6 -11 6;-6 -11 5] [auto_vectores auto_valores] = eig(A)
A =
0 1 -1
-6 -11 6
-6 -11 5
auto_vectores =
0.7071 -0.2182 -0.0921
0.0000 -0.4364 -0.5523
0.7071 -0.8729 -0.8285
auto_valores =
-1.0000 0 0
0 -2.0000 0
0 0 -3.0000
Ejercicio 8
Determinación de valores de tensión en un circuito
A = [1.5-i*2 -.35+i*1.2; -.35+i*1.2 .9-i*1.6] I = [30+i*40;20+i*15] % Resolvemos como en el ejercicio anterior V = A \ I S = V .* conj(I) % Así obtenemos las potencias deseadas
A =
-8.5000 5.6500
5.6500 -7.1000
I =
230
95
V =
-76.3257
-74.1184
S =
1.0e+04 *
-1.7555
-0.7041
Ejercicio 9
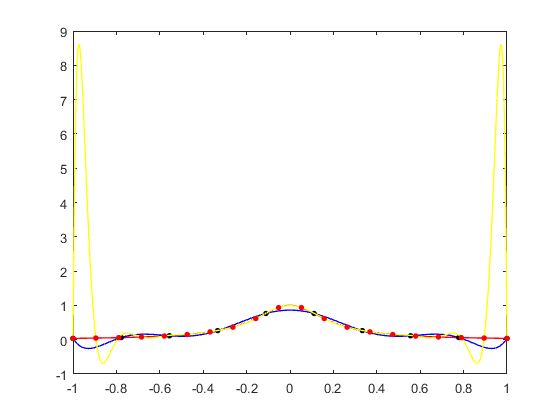
La función a la que llamamos para actuar es la siguiente: function [ answer ] = lagrang( cx,cy,x ) suma=0; for j=1:length(cx) prod=1; for i=1:length(cx) if i~=j prod=prod*(x-cx(i))/(cx(j)-cx(i)); end end suma=suma+prod*cy(j); end answer=(suma); end
f = @(x) 1./(1 + 25*x.^2); x=linspace(-1,1,500); y_true=f(x); figure; plot(x,y_true,'r','linewidth',1); hold on; N=10; xint=linspace(-1,1,N); y=f(xint); n1=length(x); yint=zeros(1,n1); for i = 1:n1 yint(i) =lagrang(xint,y,x(i)); end plot(x,yint,'k') hold on; N=20; xint=linspace(-1,1,N); y=f(xint); n1=length(x); yint=zeros(1,n1); for i = 1:n1 yint(i) =lagrang(xint,y,x(i)); end plot(x,yint,'g') hold on; %Equally spaced points N=10; xdata=linspace(-1,1,N); ydata=f(xdata); p=polyfit(xdata,ydata,N-1); y_fit=polyval(p,x); poly10=plot(x,y_fit,'b','linewidth',1); hold on; plot(xdata,ydata,'k.','markersize',12) hold on; N=20; xdata=linspace(-1,1,N); ydata=f(xdata); p=polyfit(xdata,ydata,N-1); y_fit=polyval(p,x); poly20=plot(x,y_fit,'y','linewidth',1); hold on; plot(xdata,ydata,'r.','markersize',12) hold on; % Se recomienda al usuario que si desea verlo mejor tome y modifique el % código que se recoge simplemente comentando las zonas que no desea % observar en pantalla hold off
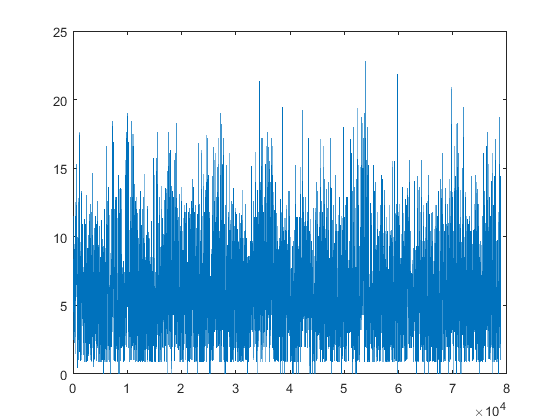
Ejercicio 10
vientos=xlsread('winddata.xlsx'); plot(vientos(:,4)) hold off
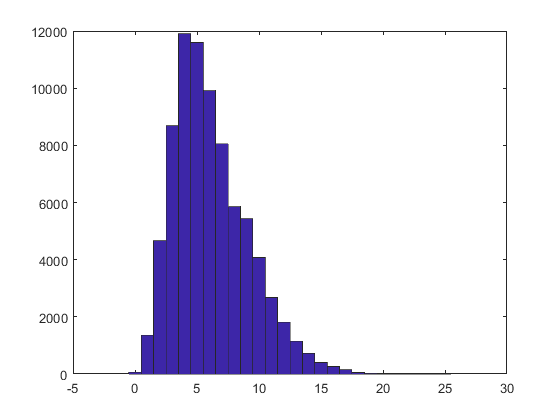
vientos=xlsread('winddata.xlsx'); numeros=0:25; hist(vientos(:,4),numeros) hold off
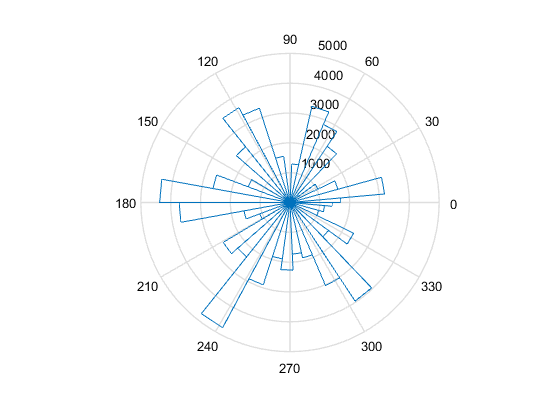
vientos=xlsread('winddata.xlsx');
numeros2=linspace(0,2*pi,36);
rose(vientos(:,4),numeros2)
Ejercicio 11
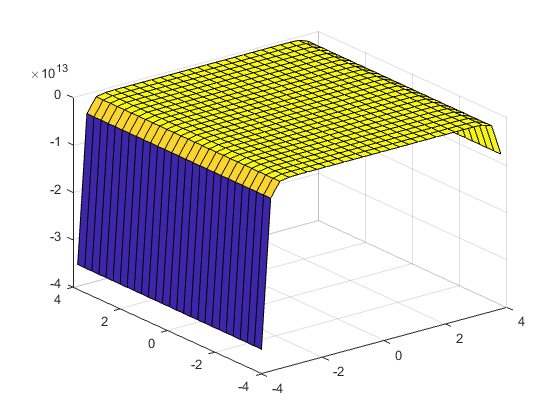
Graficar la curva tridimensional Se crea una rejilla de los puntos espaciados como se desea
hold off [x,y]=meshgrid(-4:0.3:4); % Se calculan los valores de la función para esos puntos z=sin(x)*cos(y)*exp(x.^2 + y.^2); % Se grafican y obtiene la solución surf(x,y,z) hold off
Ejercicio 12
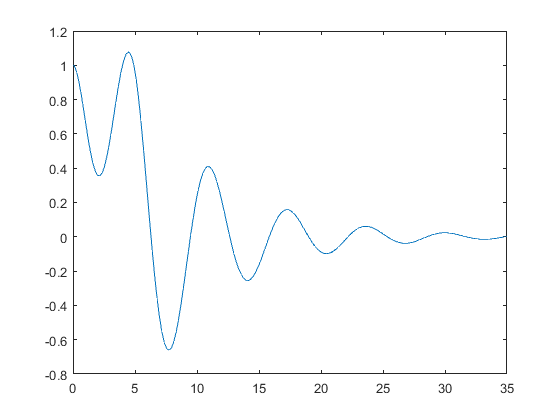
Este ejercicio lo resolvemos con una cadena de funciones. Se recogen a continuación:
% function ode % [t, yy] = ode45(@HalfSine, [0 35], [1 0], [ ], 0.15); % plot(t, yy(:,1)) % function y = HalfSine(t, y, z) % h = sin(pi*t/5).*(t<=5); % y = [y(2); -2*z*y(2)-y(1)+h]; % La llamamos para mostrarla ode % La función HalfSine introduce la forma de nuestra ecuación diferencial % mientras que ode llama a ode45, una función del sistema, y dibuja la % gráfica. en proceso obtenemos una matriz resultado yy. La primera columna % de esta función es la función que buscamos y la segunad columna es la % derivada o diferencial. hold off
Ejercicio 13
Vamos a realizar transformadas de fourier
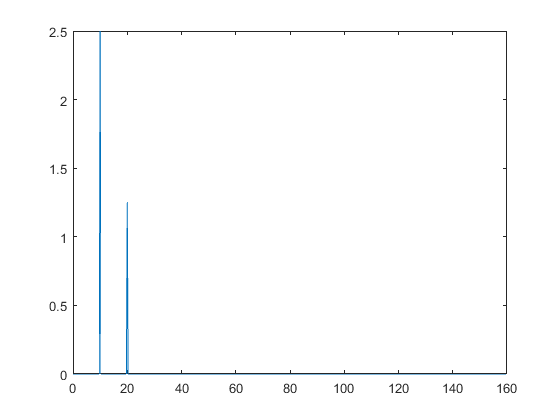
Primer apartado
k = 5; m = 10; fo = 10; Bo = 2.5; N = 2^m; T = 2^k/fo;
ts = (0:N-1)*T/N; df = (0:N/2-1)/T;
SampledSignal = Bo*sin(2*pi*fo*ts)+Bo/2*sin(2*pi*fo*2*ts);
An = abs(fft(SampledSignal, N))/N;
plot(df, 2*An(1:N/2))
hold off
Segundo apartado
k = 5; m = 10; fo = 10; Bo = 2.5; N = 2^m; T = 2^k/fo;
ts = (0:N-1)*T/N; df = (0:N/2-1)/T;
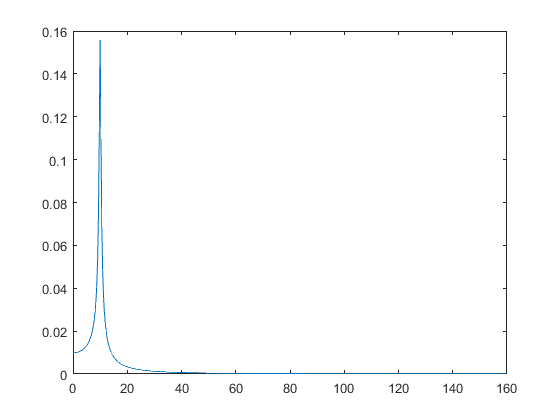
SampledSignal = exp(-2*ts).*sin(2*pi*fo*ts);
An = abs(fft(SampledSignal, N))/N;
plot(df, 2*An(1:N/2))
hold off
Tercer apartado
k = 5; m = 10; fo = 10; Bo = 2.5; N = 2^m; T = 2^k/fo;
ts = (0:N-1)*T/N; df = (0:N/2-1)/T;
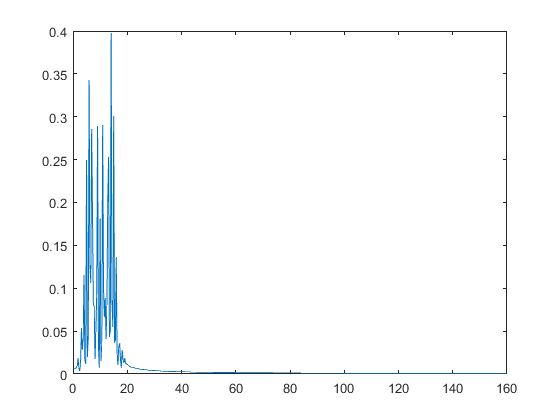
SampledSignal = sin(2*pi*fo*ts+5*sin(2*pi*fo/10*ts));
An = abs(fft(SampledSignal, N))/N;
plot(df, 2*An(1:N/2))
hold off
Cuarto apartado
k = 5; m = 10; fo = 10; Bo = 2.5; N = 2^m; T = 2^k/fo;
ts = (0:N-1)*T/N; df = (0:N/2-1)/T;
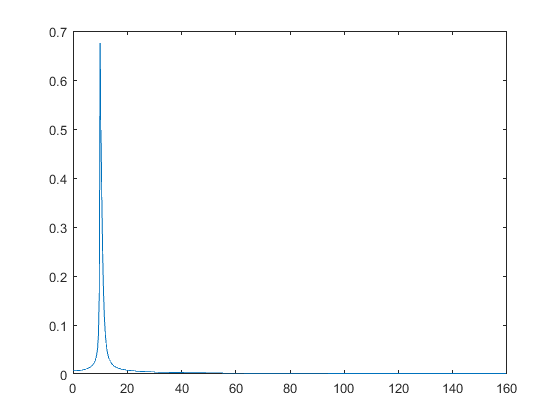
SampledSignal = sin(2*pi*fo*ts-5*exp(-2*ts));
An = abs(fft(SampledSignal, N))/N;
plot(df, 2*An(1:N/2))
hold off
Ejercicio 14
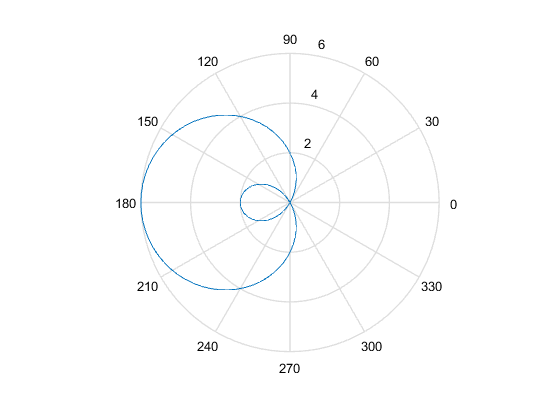
Graficar ecuacion con coordenadas polares Tomamos un conjunto de ángulos para graficar
tetha=linspace(-pi,pi,100); % Introducimos la ecuación r=2-4*cos(tetha); % Utilizamos la herramienta de matlab para dibujar polar(tetha,r) hold off
Ejercicio 15
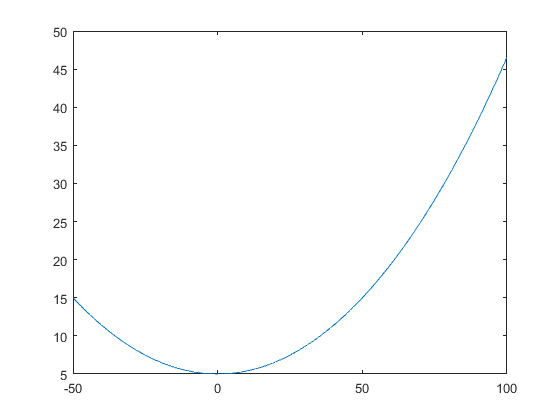
Catenaria
y = 15 ; w = 10 ; y0 = 5 ; x = 50 ; % Como utilizamos bisección necesitamos dos valores iniciales. Ta0=1000; Ta1=2000; f=inline('( x ./ 10 ) .* cosh ( ( 10 ./ x ) * 50 ) + 5 - x ./ 10 - 15 ') Ta=secante(Ta0,Ta1,f,10^-16) % Calculamos la Longitud L=2*Ta/w*sinh(2*w*50/Ta) %Graficamos la función x=-50:100; y = ( Ta / 10 ) * cosh ( ( 10 / Ta ) * x ) + 5 - Ta / 10; plot(x,y)
f =
Inline function:
f(x) = ( x ./ 10 ) .* cosh ( ( 10 ./ x ) * 50 ) + 5 - x ./ 10 - 15
Ta =
1.2663e+03
L =
221.4447